Kunci Jawaban Matematika Kelas 8 Halaman 48 Semester 2, Uji Kompetensi 6: Teorema Pythagoras

TRIBUNNEWS.COM - Berikut kunci jawaban mata pelajaran Matematika kelas 8 halaman 48 semester 2, bagian Uji Kompetensi 6.

Soal Matematika kelas 8 halaman 48 semester 2 bagian Uji Kompetensi 6 membahas materi tentang Teorema Pythagoras.

Tribunnews.com tidak bertanggung jawab dalam perbedaan jawaban pada kunci jawaban Matematika kelas 8 halaman 48 semester 2.

Berikut ini kunci jawaban Matematika kelas 8 halaman 48 semester 2, bagian Uji Kompetensi 6 soal nomor 14-17:

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 47 Semester 2, Uji Kompetensi 6: Teorema Pythagoras

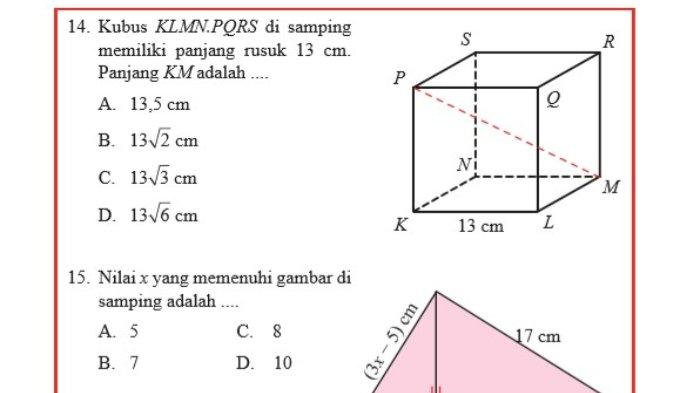
14. Kubus KLMN.PQRS di samping memiliki panjang rusuk 13 cm.

Panjang KM adalah ....

A. 13,5 cm

B. 13 √2 cm

C. 13 √3 cm

D. 13 √6 cm

Jawaban: B

Pembahasan:

Diketahui kubus KLMN.PQRS.
Panjang rusuk KL = LM = MN = NK = 13 cm.
Untuk menentukan panjang diagonal bidang KM, gunakan teorema Pythagoras, sehingga:
KM² = KL² + LM²
KM² = 13² + 13²
KM² = 169 + 169
KM² = 338
KM = √338
KM = √(169 x 2)
KM = 13√2

Jadi, panjang diagonal bidang KM adalah 13√2 cm.

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 46 Semester 2, Uji Kompetensi 6: Teorema Pythagoras

15. Nilai x yang memenuhi gambar di samping adalah ....

A. 5      C. 8

B. 7      D. 10

Jawaban: A

Pembahasan:

alas = a
tinggi = b
hipotenusa = c
b² = c² – a²
b² = 17² – 15²
b² = 289 – 225
b² = 64
b = √64
b = 8 cm

Selanjutnya mencari nilai x, cari panjang hipotenusa dengan Pythagoras:
c² = a² + b²
(3x – 5)² = 6² + 8²
(3x – 5)² = 36 + 64
(3x – 5)² = 100
3x – 5 = √100
3x – 5 = 10
3x = 10 + 5
3x = 15
x = 15 / 3
x = 5

Maka, nilai x yang memenuhi adalah 5.

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 42 Semester 2, Cara Menentukan Luas Trapesium

16. Luas daerah yang diarsir dari gambar di samping adalah ....

A. 5 dm²

B. 10 dm²

C. 12 dm²

D. 20 dm²

Jawaban: A

Pembahasan:

- Langkah pertama: hitung panjang diagonal bidang BE.

Perhatikan segitiga siku-siku ABE:
BE sebagai sisi miring;
BA dan AE sisi-sisi berpenyiku dengan panjang 40 cm dan 30 cm.
BE² = BA² + AE²
BE² = 40² + 30²
BE = √1.600 + 900
BE = √2.500
Diperoleh panjang sisi BE = 50 cm.

- Langkah kedua: hitung luas bidang diagonal BCHE
Persegi panjang BCHE memiliki panjang 50 cm dan lebar 10 cm.
Luas persegi panjang BCHE = panjang x lebar
Luas BCHE = 50 x 10
Jadi luas daerah yang diarsir, yakni luas bidang diagonal BCHE, sebesar 500 cm²
500 cm² = 5 dm²

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 45 Semester 2, Uji Kompetensi 6: Teorema Pythagoras

17. Perhatikan limas T.ABCD di samping. Alas limas berbentuk persegi dengan panjang sisi 14 cm dan panjang TO = 24 cm. Panjang TE adalah ....

A. 25 cm

B. 26 cm

C. 27 cm

D. 28 cm

Jawaban: A

Pembahasan:

Diketahui:
AB = 14 cm
OE = 1/2 × AB = 1/2 × 14 cm = 7 cm
TO = 24 cm

Ditanya: Panjang TE =… ?
Jawab :
TE² = TO² + OE²
= 24² + 7²
= 576 + 49
= 625
TE = √625
= 25 cm
Jadi, panjang TE adalah 25 cm

*) Disclaimer:

- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.

- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(Tribunnews.com/Nurkhasanah)