Kunci Jawaban Matematika Kelas 12 Halaman 232 Semester 2: Uji Kompetensi Nomor 5-10 Kesebangunan

TRIBUNNEWS.COM - Berikut kunci jawaban Matematika kelas 12 semester 2 halaman 232.

Pada Buku Matematika kelas 12 halaman 232, terdapat soal uji kompetensi tentang kongruen dan kesebangunan.

Jawaban dari soal tersebut akan dibahas di bawah ini, tetapi ada baiknya siswa tidak menjadikan artikel ini sebagai acuan.

Siswa lebih baik mencoba menjawab sendiri terlebih dahulu dengan bantuan orang tua.

Kunci jawaban soal Matematika kelas 12 halaman 232 semester 2 soal uji kompetensi nomor 5-10:

Baca juga: Kunci Jawaban Tema 5 Kelas 2 Halaman 86 Semester 2: Mengukur Sapu Lidi hingga Kemoceng

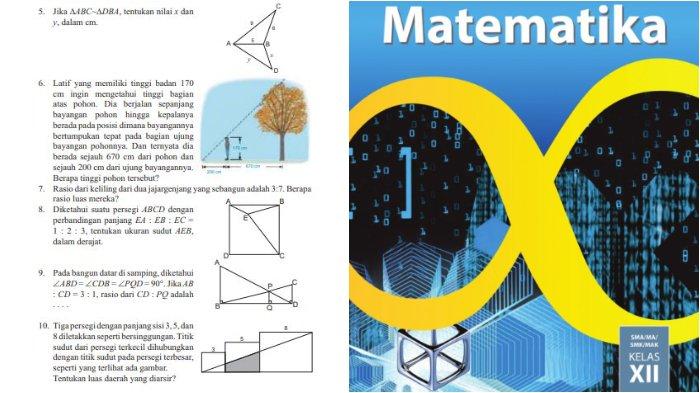
5. Jika ∆ABC ~ ∆DBA, tentukan nilai x dan y, dalam cm.

Jawaban:

x/6 = 5/5 sehingga x = 6

y/9 = 5/5 sehingga y = 9

6. Latif yang memiliki tinggi badan 170 cm ingin tahu tinggi bagian atas pohon. Dia berjalan sepanjang banyangan pohon hingga kepalanya berada di posisi di mana bayangannya bertumpukan tepat pada bagian ujung bayangan pohonnya. Dan ternyata dia berada sejauh 670 cm dari pohon dan sejauh 200 dari ujung bayangannya. Berapa tinggi pohon tersebut?

Jawaban:

Misal tinggi pohon adalah y cm

y/170 = 870/200 sehingga y = 170x870 / 200 = 739,5 cm

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 220 Semester 2, Uji Kompetensi 8: Bangun Ruang Sisi Datar

7. Rasio dari keliling dari dua jajargenjang yang sebangun adalah 3:7. Berapa rasio luas mereka?

Jawaban:

Karena rasio kelilingnya 3:7, maka rasio ukuran panjang sisi-sisi yang bersesuaian juga 3:7, dengan demikian rasio dari luasnya adalah 32 :72 = 9:49.

8. Diketahui suatu persegi dengan perbandingan panjang, tentukan ukuran sudut, dalam derajat.

Jawaban:

Putar dengan pusat putar di B sebesar 90  berlawanan arah jarum jam, seperti pada gambar. Hubungkan EE’.

Sehingga ∆BEE’ adalah segitiga siku-siku sama kaki dan oleh karena itu, ∠BE’E = 45 dan panjang EE’ adalah Sehingga  ∆CEE’ adalah segitiga siku-siku, dengan menerapkan teorema Pythagoras didapat ∠CE’E = 90. Kita punya ∠AEB = ∠CE’ ∠BE’E = 90 + 45 = 135.

Baca juga: Kunci Jawaban Matematika Kelas 12 Halaman 231 Semester 2: Uji Kompetensi Nomor 1-4 Tentang Kongruen

9. Pada bangun datar di samping, diketahui ∠ABD = ∠CDB = ∠PQD = 90  . Jika AB:CD = 3:1, rasio dari CD:PQ adalah …

Jawaban:

Misal BQ= a dan DQ = b, seperti yang ditunjukkan bangun datar berikut.

Berdasarkan konjektur kesebangunan segitiga (Sudut-Sudut-Sudut), segitiga ABD dan segitiga PQD sebangun sehingga PQ/AB = b/(a+b)

Berdasarkan konjektur kesebangunan segitiga (Sudut-Sudut-Sudut), segitiga CBD dan segitiga PBD sebangun sehingga PQ/CD = a/(a+b)  

Dengan membagi persamaan kedua dengan persamaan pertama, kita dapatkan persamaan AB/CD = a/b = 3. Dengan demikian, CD/PQ = (a+b)/a = 4/3.

Baca juga: Kunci Jawaban Bahasa Indonesia Kelas 8 Halaman 54 Semester 2 Bagian B: Buatlah Sebuah Iklan

10. Tiga persegi dengan Panjang sisi 3, 5, dan 8 diletakkan seperti bersinggungan. Titik sudut dari persegi terkecil dihubungkan dengan titik sudut dari persegi terkecil dihubungkan dengan titik sudut pada persegi terbesar, seperti yang terlihat pada gambar. Tentukan luas daerah yang diarsir!

Jawaban:

Pada segitiga ∆ABE dan ∆ADG, berdasarkan konjektur kesebangunan segitiga Sudut-Sudut, maka segitiga ∆ABE dan ∆ADG kongruen.

Sehingga AB/BE = AD/DG, BE = 3/2.

Dan berdasarkan konjektur kesebangunan segitiga Sudut-Sudut, maka segitiga ∆ABE dan ∆ACF kongruen.

Sehingga AB/BE = AC/CF, CF = 4.

Dengan demikian, luas segiempat EBFC = luas ∆ACF – luas ∆ABE

                                                            = 1/2.8.4 – 1/2. 3. 3/2 = 16 – 9/4 = 15/4

*) Disclaimer:Jawaban di atas hanya digunakan untuk memandu proses belajar anak.

Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(Tribunnews.com/Isti Prasetya)