Kunci Jawaban Matematika Kelas 12 Halaman 231 Semester 2: Uji Kompetensi Nomor 1-4 Tentang Kongruen

TRIBUNNEWS.COM - Berikut kunci jawaban Matematika kelas 12 semester 2 halaman 231.

Pada Buku Matematika kelas 12 halaman 231 terdapat soal uji kompetensi tentang kongruen dan kesebangunan.

Jawaban dari soal tersebut akan dibahas di bawah ini, tetapi ada baiknya siswa tidak menjadikan artikel ini sebagai acuan.

Siswa lebih baik mencoba menjawab sendiri terlebih dahulu dengan bantuan orangtua.

Kunci jawaban soal Matematika kelas 12 halaman 231 semester 2 soal uji kompetensi:

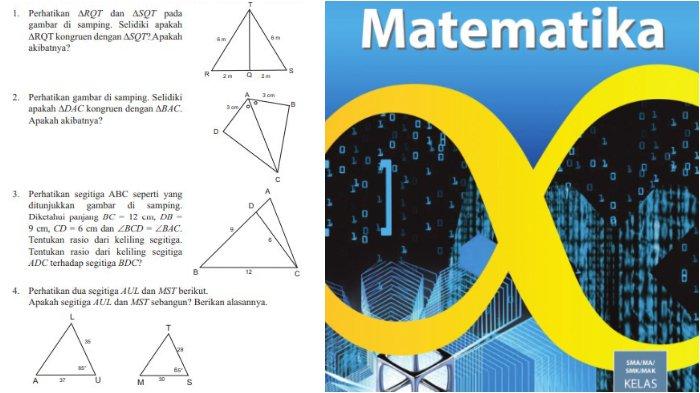
1. Perhatikan ∆RQT dan ∆SQT pada gambar di samping. Selidiki apakah ∆RQT kongruen dengan ∆SQT? Apakah akibatnya?

Jawaban:

Karena RT = ST, RQ = SQ, TQ = TQ, maka ketiga sisi yang bersesuaian sama Panjang. Berdasarkan konjektur kekongruenan Sudut-Sudut-Sudut, ∆RQT ≅ ∆SQT.

Akibatnya besar ∠R = ∠S, ∠RTQ = ∠STQ dan ∠TQR = ∠TQS.

Baca juga: Kunci Jawaban Bahasa Inggris Kelas 12 Halaman 86 87 Semester 2, Task 3: Comprehension Questions

2. Perhatikan gambar di samping. Selidiki apakah ∆DAC kongruen dengan ∆BAC. Apakah akibatnya?

Jawaban:

Perhatikan ∆DAC dan ∆BAC.

Karena DA = BA,  ∠ DAC = ∠ BAC dan AC = AC, maka berdasarkan konjektur kekongruenan segitiga Sisi-Sudut-Sisi, ∆DAC ≅ ∆BAC.

Akibatnya CD = BC, ∠ADC = ∠ABC, ∠DCA = ∠BCA

Baca juga: Kunci Jawaban Matematika Kelas 12 Halaman 150 Semester 2: Uji Kompetensi Nomor 1-5 Faktorial

3. Perhatikan segitiga ABC seperti yang ditunjukkan gambar di samping. Diketahui panjang BC = 12 cm, DB = 9 cm, CD = 6 cm dan ∠BCD = ∠BAC. Tentukan rasio dari keliling segitiga. Tentukan rasio dari keliling segitiga ADC terhadap segitiga BCD?