Kunci Jawaban Matematika Kelas 8 Halaman 312 Semester 2, Uji Kompetensi Semester 2

TRIBUNNEWS.COM - Berikut kunci jawaban mata pelajaran Matematika kelas 8 halaman 312 semester 2, bagian Uji Kompetensi Semester 2.

Soal Matematika kelas 8 halaman 312 semester 2, bagian Uji Kompetensi Semester 2.

Tribunnews.com tidak bertanggung jawab dalam perbedaan jawaban pada kunci jawaban Matematika kelas 8 halaman 312 semester 2.

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 311 Semester 2, Uji Kompetensi Semester 2

Berikut kunci jawaban Matematika kelas 8 halaman 312 semester 2, bagian Uji Kompetensi Semester 2 soal pilihan ganda nomor 4-7:

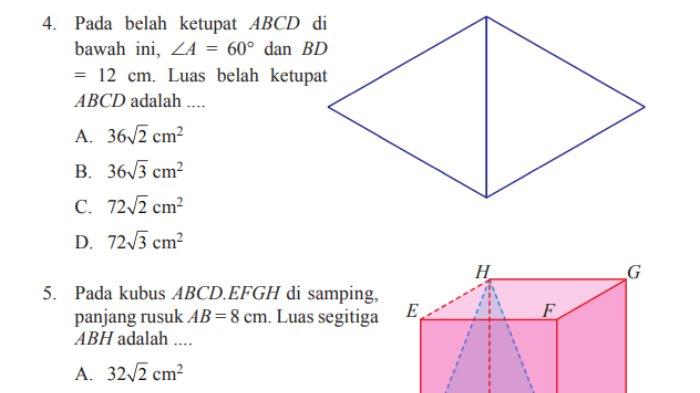
4. Pada belah ketupat ABCD di bawah ini, ∠A = 60° dan BD = 12 cm. Luas belah ketupat ABCD adalah ....

A. 36√2 cm²
B. 36√3 cm²
C. 72√2 cm²
D. 72√3 cm²

Jawaban: D

Pembahasan:

Segitiga sama sisi

Luas belah ketupat = 2 × luas segitiga sama sisi
= 2 × ( 1/2 × 12 × 12 × sin 60°)
= 144 (1/2√3)
= 72√3 cm²

5. Pada kubus ABCD.EFGH di samping, panjang rusuk AB = 8 cm. Luas segitiga ABH adalah ....

A. 32√2 cm²
B. 32√3 cm²
C. 64√2 cm²
D. 64√3 cm²

Jawaban: A

Pembahasan:

- Menghitung panjang AH

AH² = AD² + DH²
AH² = 8² + 8²
AH² = 64 + 64
AH² = 2 (64)
AH = √64 x 2
AH = 8√2 cm

- Menentukan panjang BH

BH² = AB² + BC² + BF²
BH² = 8² + 8² + 8²
BH² = 64 + 64 + 64
BH² = 3 (64)
BH = √64 x 3
BH = 8√3 cm

Segitiga ABH merupakan segitiga siku-siku yang garis AB dan AH saling tegak lurus dan siku-siku di A.

Luas Δ ABH = 1/2 × AB × AH
                     = 1/2 × 8 cm × 8√2 cm
                     = 32√2 cm²

Jadi, luas Δ ABH adalah 32√2 cm².

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 310 Semester 2, Uji Kompetensi 10: Peluang

6. Diketahui suatu juring lingkaran dengan ukuran sudut pusat 90°. Jika luas juring tersebut adalah 7.850, jari-jari lingkaran tersebut adalah .... cm. (π = 3,14)

A. 10
B. 100
C. 7
D. 49

Jawaban: B

Pembahasan:

Luas juring = α/360 x π x r²
7.850 cm² = 90/360 x 3,14 x r²
7.850 cm² = 282,6/360 x r²
r² = 7.850 : 282,2/360
r² = 7.850 × 360/282,6
r² = 2.826.000/282,6
r² = 10.000
r = √10.000
r = 100 cm

Jadi, jari-jari lingkaran tersebut adalah 100 cm.

Baca juga: Kunci Jawaban Matematika Kelas 8 Halaman 308 309 Semester 2, Uji Kompetensi 10: Peluang

7. Diketahui panjang busur suatu lingkaran adalah 43,96 cm. Jika sudut pusat yang menghadap busur tersebut berukuran 60°, panjang jari-jari juring lingkaran tersebut adalah ... cm. (π =22/7)

A. 7
B. 14
C. 21
D. 42

Jawaban: D

Pembahasan:

α/360° × 2πr = Panjang busur
60°/360° × 2 × 22/7 × r = 43,96
1/6 × 44/7 × r = 43,96
44/42 × r = 43,96
r = 43,96 : 44/42
r = 43,96 × 42/44
r = 1846,32/44
r = 41,9618...
r = 41,96 cm
r = 42 cm

Jadi, panjang jari-jari juring lingkaran tersebut adalah 42 cm.

*) Disclaimer:

- Artikel ini hanya ditujukan kepada orang tua untuk memandu proses belajar anak.

- Sebelum melihat kunci jawaban, siswa harus terlebih dahulu menjawabnya sendiri, setelah itu gunakan artikel ini untuk mengoreksi hasil pekerjaan siswa.

(Tribunnews.com/Nurkhasanah)